Poradnik bazy danych wektorowych Qdrant

Baza danych wektorów to stosunkowo nowy sposób interakcji z abstrakcyjnymi reprezentacjami danych, pochodzącymi z nieprzejrzystych modeli uczenia maszynowego, takich jak struktury głębokiego uczenia. Te reprezentacje są powszechnie nazywane wektorami lub wektorami osadzeń i stanowią spakowane wersje danych używanych do szkolenia modeli uczenia maszynowego w celu wykonywania zadań, takich jak analiza sentymentu, rozpoznawanie mowy i detekcja obiektów.

Te nowe bazy danych wykazały wybitne osiągnięcia w wielu zastosowaniach, takich jak semantyczne wyszukiwanie i systemy rekomendacyjne.

Czym jest Qdrant?

Qdrant to otwarta baza danych wektorów zaprojektowana dla aplikacji sztucznej inteligencji nowej generacji. Jest to gotowe do pracy w chmurze rozwiązanie, które zapewnia interfejsy API RESTful i gRPC do zarządzania osadzeniami. Qdrant posiada potężne funkcje, wspierając wyszukiwanie obrazów, dźwięku i wideo, a także integrację z silnikami sztucznej inteligencji.

Czym jest baza danych wektorów?

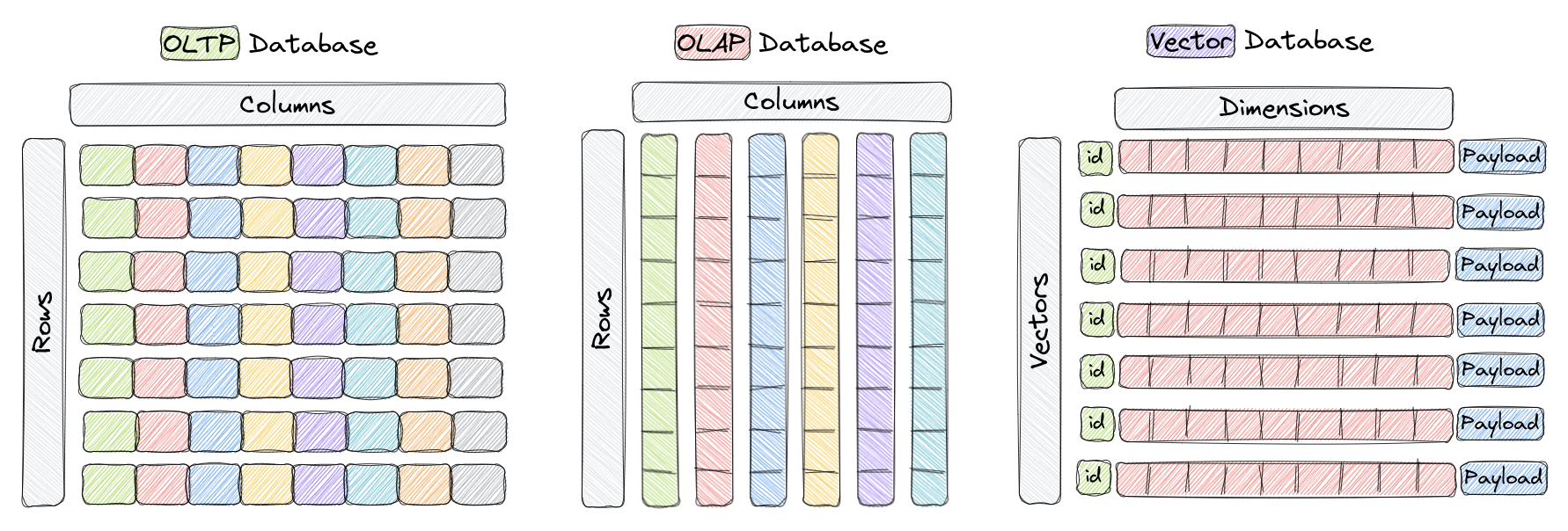
Baza danych wektorów to rodzaj bazy danych specjalnie zaprojektowanej do efektywnego przechowywania i zapytywania wysokowymiarowych wektorów. W tradycyjnych bazach danych OLTP i OLAP (jak pokazano na powyższym obrazku), dane są zorganizowane w wiersze i kolumny (zwane tabelami), a zapytania oparte są na wartościach w tych kolumnach. Jednakże w pewnych aplikacjach, takich jak rozpoznawanie obrazów, przetwarzanie języka naturalnego i systemy rekomendacyjne, dane są często reprezentowane w postaci wektorów w przestrzeni wysokowymiarowej. Te wektory, wraz z identyfikatorem i ładunkiem, stanowią elementy przechowywane w bazach danych wektorów, takich jak Qdrant.

W tym kontekście wektor stanowi matematyczną reprezentację obiektu lub punktu danych, gdzie każdy element wektora odpowiada cechom lub atrybutowi obiektu. Na przykład w systemie rozpoznawania obrazów wektor może reprezentować obraz, a każdy element wektora reprezentuje wartości pikseli lub cechę/opis piksela. W systemie rekomendacji muzycznej każdy wektor reprezentuje utwór, a każdy element wektora reprezentuje cechę utworu, taką jak rytm, gatunek, teksty, itp.

Bazy danych wektorów są zoptymalizowane pod kątem efektywnego przechowywania i zapytywania wysokowymiarowych wektorów, często wykorzystując specjalizowane struktury danych i techniki indeksowania, takie jak Hierarchical Navigable Small World (HNSW) do przybliżonego wyszukiwania najbliższych sąsiadów oraz kwantyzację produktu. Te bazy danych umożliwiają użytkownikom znalezienie najbliższych wektorów do danego wektora zgodnie z określoną metryką odległości, umożliwiając szybkie wyszukiwanie podobieństwa i semantyczne wyszukiwanie. Najczęściej stosowane metryki odległości obejmują odległość euklidesową, podobieństwo kosinusowe i iloczyn skalarny, wszystkie w pełni obsługiwane w Qdrant.

Oto krótka prezentacja tych trzech algorytmów podobieństwa wektorów:

• Podobieństwo kosinusowe - Podobieństwo kosinusowe jest miarą podobieństwa między dwoma elementami. Można je postrzegać jako miarę służącą do określania odległości między dwoma punktami; jednakże zamiast mierzyć odległość, mierzy podobieństwo między dwoma elementami. Jest powszechnie stosowane do porównywania podobieństwa między dwoma dokumentami lub zdaniami w tekście. Zakres wyniku podobieństwa kosinusowego wynosi od 0 do 1, gdzie 0 oznacza całkowite różnice, a 1 oznacza całkowite podobieństwo. Jest to prosty i skuteczny sposób porównywania dwóch elementów!
• Iloczyn skalarny - Podobieństwo iloczynu skalarnego jest inną miarą podobieństwa między dwoma elementami, podobnie jak podobieństwo kosinusowe. W przypadku liczb jest często stosowane w uczeniu maszynowym i naukach o danych. Podobieństwo iloczynu skalarnego oblicza się poprzez mnożenie wartości w dwóch zestawach liczb, a następnie dodanie tych iloczynów. Wyższa suma wskazuje wyższe podobieństwo między dwoma zestawami liczb. Jest to jak skala mierząca stopień dopasowania między dwoma zestawami liczb.
• Odległość euklidesowa - Odległość euklidesowa to sposób mierzenia odległości między dwoma punktami w przestrzeni, podobnie jak mierzymy odległość między dwoma miejscami na mapie. Oblicza się ją poprzez znalezienie pierwiastka kwadratowego sumy kwadratów różnic między współrzędnymi dwóch punktów. Ta metoda pomiaru odległości jest powszechnie stosowana w uczeniu maszynowym do oceny podobieństwa lub różnorodności dwóch punktów danych, innymi słowy, do zrozumienia, jak daleko są od siebie.

Teraz, kiedy wiemy, czym są bazy danych wektorów i w jaki sposób różnią się strukturalnie od innych baz danych, spróbujmy zrozumieć, dlaczego są ważne.

Dlaczego potrzebujemy bazy danych wektorów?

Bazy danych wektorów odgrywają kluczową rolę w różnych aplikacjach, które wymagają wyszukiwania podobieństw, takich jak systemy rekomendacyjne, wyszukiwanie obrazów opartych na treści oraz spersonalizowane wyszukiwanie. Dzięki wykorzystaniu efektywnych technik indeksowania i wyszukiwania, bazy danych wektorów mogą szybciej i dokładniej odzyskiwać niestrukturyzowane dane reprezentowane jako wektory, prezentując najbardziej istotne wyniki zapytań użytkownika.

Dodatkowe korzyści z korzystania z bazy danych wektorów obejmują:

1. Efektywne przechowywanie i indeksowanie danych o wysokiej wymiarowości.
2. Możliwość obsługi dużych zbiorów danych zawierających miliardy punktów danych.
3. Wsparcie dla analizy i zapytań w czasie rzeczywistym.
4. Możliwość obsługi wektorów pochodzących z złożonych typów danych, takich jak obrazy, filmy i teksty w języku naturalnym.
5. Poprawa wydajności aplikacji uczenia maszynowego i sztucznej inteligencji przy jednoczesnym zmniejszeniu opóźnień.
6. Redukcja czasu i kosztów związanych z tworzeniem i wdrażaniem rozwiązań niestandardowych w porównaniu z budową dedykowanych rozwiązań.

Należy jednak pamiętać, że konkretne korzyści z korzystania z bazy danych wektorów mogą się różnić w zależności od przypadków użycia organizacji oraz wybranych funkcjonalności bazy danych.

Następnie przeprowadźmy ogólną ocenę architektury Qdrant.

Ogólny przegląd architektury Qdrant

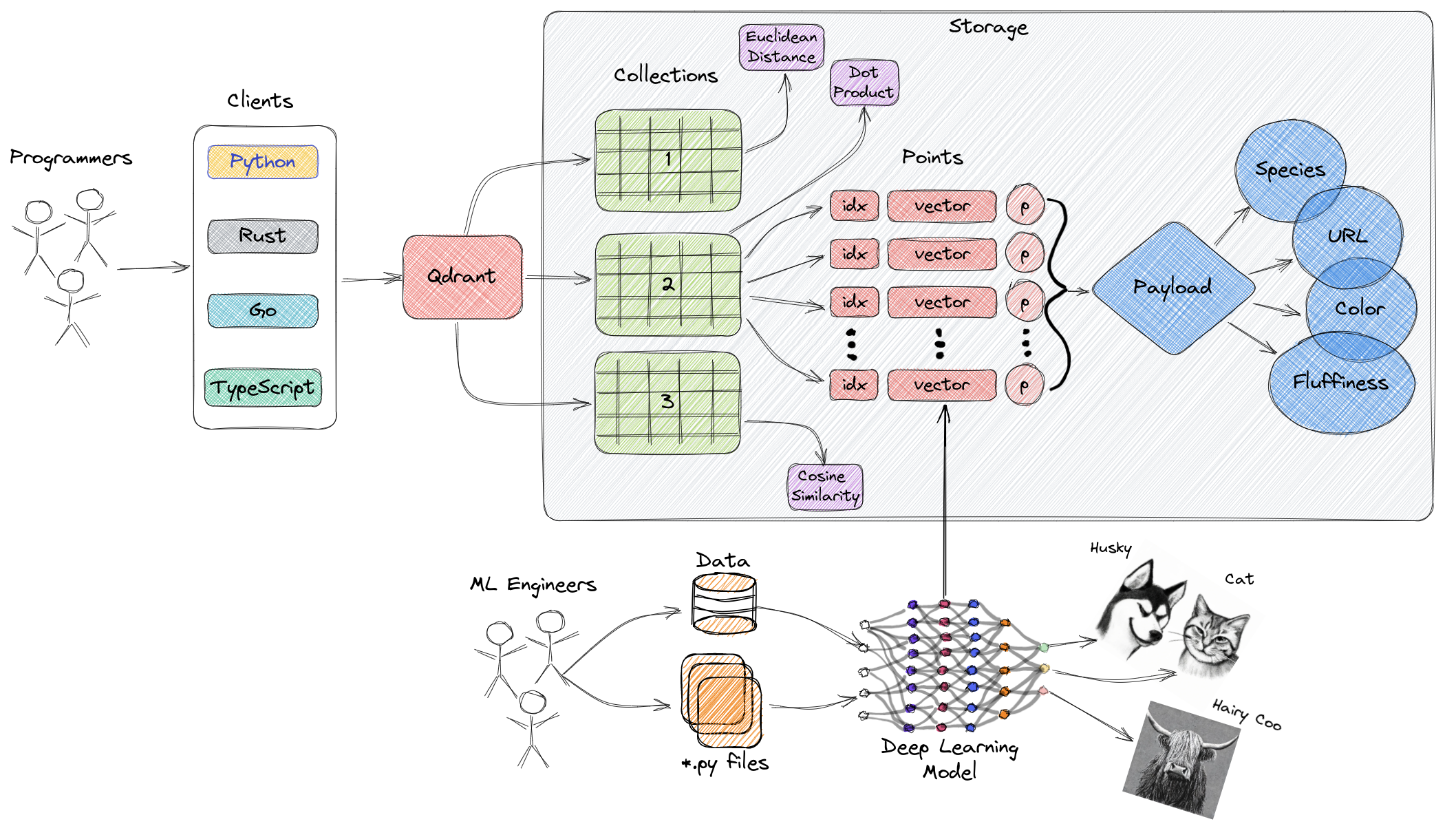
Powyższy diagram przedstawia ogólny przegląd głównych komponentów Qdrant. Oto kluczowe terminy związane z Qdrant:

• Kolekcje: Kolekcje to grupa nazwanych punktów (wektorów z ładunkami - w zasadzie danych wektorowych). W prostszych terminach, kolekcje są podobne do tabel w MySQL, a punkty są podobne do wierszy danych w tych tabelach. Wśród tych punktów można przeprowadzać wyszukiwanie. Każdy wektor w tej samej kolekcji musi mieć tę samą liczbę wymiarów i być porównywany za pomocą jednej metryki. Nazwane wektory mogą być używane do umieszczenia wielu wektorów w jednym punkcie, z własnymi wymiarami i wymaganiami dotyczącymi metryki.
• Metryka: Miara używana do kwantyfikowania podobieństwa pomiędzy wektorami, która musi być wybrana podczas tworzenia kolekcji. Wybór metryki zależy od metody pozyskiwania wektorów, szczególnie dla sieci neuronowych używanych do kodowania nowych zapytań (metryka to algorytm podobieństwa, który wybieramy).
• Punkty: Punkt to podstawowa jednostka operacyjna w Qdrant, składająca się z wektorów, opcjonalnego identyfikatora (ID) i ładunków (podobne do wierszy danych w tabeli MySQL).
  • ID: Unikalny identyfikator wektora.
  • Wektor: Wysokowymiarowe przedstawienie danych, takich jak obrazy, dźwięk, dokumenty, filmy itp.
  • Ładunek: Obiekt JSON, który można dodać do wektora jako dodatkowe dane (głównie używane do przechowywania właściwości biznesowych związanych z wektorem).
• Przechowywanie: Qdrant może korzystać z dwóch opcji przechowywania - przechowywania w pamięci (wszystkie wektory przechowywane w pamięci, co zapewnia najwyższą prędkość, ponieważ dostęp do dysku jest używany tylko do trwałości) oraz przechowywania Memmap (tworzenie przestrzeni adresowej wirtualnie powiązanej z plikami na dysku).
• Klienci: Można połączyć się z Qdrant za pomocą pakietów SDK języków programowania lub bezpośrednio komunikować się z Qdrant za pomocą jego interfejsu API REST.